変圧器の等価回路 -自己インダクタンスと相互インダクタンス-

 

前書き

この記事では結合インダクタを表現するために頻繁に使用される自己・相互インダクタンス（結合係数）を用いて、変圧器の等価回路を算出する。算出したT型等価回路は等価回路中の理想変圧器の変圧比を任意に与えることで、自由に１次・２次直列インダクタンスの値を調整可能な電気的に等価な回路を得ることができる。算出した等価回路と漏れ・励磁インダクタンスを用いた等価回路を比較して、変圧器の実際の巻き数比を用いることで、自己・相互インダクタンスと漏れ・励磁インダクタンスを相互に変換する式を求める。

結合インダクタ

2つのコイルが結合しており、1次側コイルの電圧を$v_{1}$、電流を$i_{1}$、2次側コイルの電圧を$v_{2}$、電流を$i_{2}$とする。$i_{1}$によって励磁される1次コイルの磁束を$\phi_{1}$、$i_{2}$によって励磁される2次コイルの磁束を$\phi_{2}$とする。$\phi_{1}$の中で2次コイルに鎖交する磁束を$\phi_{21}$、$\phi_{2}$の中で1次コイルに鎖交する磁束を$\phi_{12}$とする。

自己インダクタンスと相互インダクタンス

1次側コイルに鎖交する全磁束は$\phi_{1} + \phi_{12}$であるため、ファラデーの法則より$v_{1}$は次式で得られる。ここで1次側コイルの巻き数を$N_{1}$とする。

\begin{equation} v_{1} = N_{1} \frac{d}{dt} \left( \phi_{1} + \phi_{12} \right) \end{equation}

磁束$\phi_{1}$、$\phi_{12}$の$N_{1}$倍はそれぞれ$i_{1}$、$i_{2}$によって励磁されるため、これらの電流に比例する。それぞれの比例定数を$L_{11}$、$M_{12}$とする。

\begin{align} N_{1} \phi_{1} &= L_{11} i_{1} \\ N_{1} \phi_{12} &= M_{12} i_{2} \end{align}

ここで$L_{11}$を1次コイルの自己インダクタンス、$M_{12}$を相互インダクタンスと呼ぶ。これらの式から、1次側コイルの電圧電流関係式が得られる。

\begin{equation} v_{1} = L_{11} \frac{d i_{1}}{dt} + M_{12} \frac{d i_{2}}{dt} \end{equation}

2次側コイルの電圧電流関係式も同様にして下式で得られる。ここで$L_{22}$を2次コイルの自己インダクタンス、$M_{21}$を相互インダクタンスとする。

\begin{equation} v_{2} = L_{22} \frac{d i_{2}}{dt} + M_{21} \frac{d i_{1}}{dt} \end{equation}

相互インダクタンスの相反定理より

\begin{equation} M = M_{12} = M_{21} \end{equation}

結合係数

結合係数$k$は次式で定義される。

\begin{equation} M = k \sqrt{L_{11} L_{22}} \end{equation}

よって$M$の代わりに$k$を用いて、変圧器の電圧・電流関係式は次式で表すこともできる。

\begin{align} v_{1} &= L_{11} \frac{d i_{1}}{dt} + k \sqrt{L_{11} L_{22}} \frac{d i_{2}}{dt} \\ v_{2} &= k \sqrt{L_{11} L_{22}} \frac{d i_{1}}{dt} + L_{22} \frac{d i_{2}}{dt} \end{align}

$k = 0$のとき、変圧器の電圧・電流関係式は次式となり、1次・2次コイルは結合しない。

\begin{align} v_{1} &= L_{11} \frac{d i_{1}}{dt} \\ v_{2} &= L_{22} \frac{d i_{2}}{dt} \end{align}

また$k=1$のとき、1次・2次側電圧の比は

\begin{equation} \frac{v_{2}}{v_{1}} = \sqrt{\frac{L_{22}}{L_{11}}} = N_{12}^{\ast} \end{equation}

となり、1次・2次側自己インダクタンスの比の平方根に等しい。この1次・2次側自己インダクタンスの比の平方根を$N_{12}^{\ast}$とする。

等価回路

自己インダクタンスと結合係数によるL型等価回路

自己・相互インダクタンスを用いた、変圧器の電圧・電流関係式を再掲する。

\begin{align} v_{1} &= L_{11} \frac{d i_{1}}{dt} + M \frac{d i_{2}}{dt} \\ v_{2} &= L_{22} \frac{d i_{2}}{dt} + M \frac{d i_{1}}{dt} \end{align}

上式を次のように変形する。

\begin{align} v_{1} &= L_{11} \frac{d}{dt} \left( i_{1} + \frac{M}{L_{11}} i_{2} \right) \\ v_{2} &= \frac{M}{L_{11}} \left\{ L_{11} \frac{d}{dt} \left( i_{1} + \frac{M}{L_{11}} i_{2} \right) + \left( \frac{L_{11} L_{22}}{M^{2}} - 1 \right) L_{11} \frac{d}{dt} \frac{M}{L_{11}} i_{2} \right\} \end{align}

上式より、下図のL型等価回路が得られる。

上式の相互インダクタンスを結合係数に置き換えると次式のように表せるため、下図のL型等価回路に変形することも可能であることがわかる。

\begin{align} v_{1} &= L_{11} \frac{d}{dt} \left( i_{1} + k \sqrt{\frac{L_{22}}{L_{11}}} i_{2} \right) \notag \\ &= L_{11} \frac{d}{dt} \left( i_{1} + k N_{12}^{\ast} i_{2} \right) \\ v_{2} &= k \sqrt{\frac{L_{22}}{L_{11}}} \left\{ L_{11} \frac{d}{dt} \left( i_{1} + k \sqrt{\frac{L_{22}}{L_{11}}} i_{2} \right) + \left( \frac{1}{k^{2}} - 1 \right) L_{11} \frac{d}{dt} k \sqrt{\frac{L_{22}}{L_{11}}} i_{2} \right\} \notag \\ &= k N_{12}^{\ast} \left\{ L_{11} \frac{d}{dt} \left( i_{1} + k N_{12}^{\ast} i_{2} \right) + \left( \frac{1}{k^{2}} - 1 \right) L_{11} \frac{d}{dt} k N_{12}^{\ast} i_{2} \right\} \notag \\ &= k N_{12}^{\ast} L_{11} \frac{d}{dt} \left( i_{1} + k N_{12}^{\ast} i_{2} \right) + \left( 1 - k^{2} \right) L_{22} \frac{d i_{2}}{dt} \end{align}

この図より、L型等価回路モデルでは、励磁インダクタンスに相当するのは自己インダクタンス$L_{11}$であり、漏れインダクタンスに相当するのは結合係数と自己インダクタンスを用いた$(1 - k^{2})L_{22}$としている。

自己インダクタンスと結合係数によるT型等価回路

変圧器の電圧・電流関係式を再掲する。

\begin{align} v_{1} &= L_{11} \frac{d i_{1}}{dt} + k \sqrt{L_{11} L_{22}} \frac{d i_{2}}{dt} \\ v_{2} &= L_{22} \frac{d i_{2}}{dt} + k \sqrt{L_{11} L_{22}} \frac{d i_{1}}{dt} \end{align}

自己インダクタンスと結合係数を用いたT型等価回路を構成するためには、等価回路の中の理想変圧器の変圧比を任意に与える必要がある。この変圧比を$N_{12}^{\dagger}$と与える場合、上式を次のように変形する。

\begin{align} v_{1} &= \left( L_{11} - \frac{k \sqrt{L_{11} L_{22}}}{N_{12}^{\dagger}} \right) \frac{d i_{1}}{dt} + \frac{k \sqrt{L_{11} L_{22}}}{N_{12}^{\dagger}} \frac{d}{dt} \left( i_{1} + N_{12}^{\dagger} i_{2} \right) \notag \\ &= \left( 1 - k \frac{N_{12}^{\ast}}{N_{12}^{\dagger}} \right) L_{11} \frac{d i_{1}}{dt} + k L_{11} \frac{N_{12}^{\ast}}{N_{12}^{\dagger}} \frac{d}{dt} \left( i_{1} + N_{12}^{\dagger} i_{2} \right) \end{align}

\begin{align} v_{2} &= \left( L_{22} - k L_{11} N_{12}^{\ast} N_{12}^{\dagger} \right) \frac{d i_{2}}{dt} + k L_{11} N_{12}^{\ast} \frac{d}{dt} \left( i_{1} + N_{12}^{\dagger} i_{2} \right) \notag \\ &= \left( 1 - k \frac{N_{12}^{\dagger}}{N_{12}^{\ast}} \right) L_{22} \frac{d i_{2}}{dt} + k L_{11} N_{12}^{\ast} \frac{d}{dt} \left( i_{1} + N_{12}^{\dagger} i_{2} \right) \end{align}

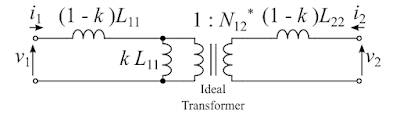
よって上図の等価回路が得られる。この等価回路の各パラメータは、$N_{12}^{\dagger}$が変圧器の巻き数比である場合を除いて、物理的な意味を持っておらず、各部のインダクタや電流などから変圧器の磁束などを計算することはできない。インダクタンスが負の値になることもある。一方で、任意の$N_{12}^{\dagger}$としても、電気回路的な性質は変化しない。よく用いられるのは$N_{12}^{\dagger}=N_{12}^{\ast}, 1$の2種類である。それぞれの等価回路は下図のようになり、$N_{12}^{\dagger}=1$の場合には理想変圧器が不要となる。

自己・相互インダクタンスと励磁・漏れインダクタンス

自己・相互インダクタンスのT型等価回路

変圧器の実際の巻き数比を$N_{12}$として、$N_{12}^{\dagger} = N_{12}$の場合を考える。

\begin{equation} N_{12} = \frac{N_{2}}{N_{1}} \end{equation}

このときの変圧器の電圧電流関係式は次式で表される。

\begin{align} v_{1} &= \left( 1 - k \frac{N_{12}^{\ast}}{N_{12}} \right) L_{11} \frac{d i_{1}}{dt} + k L_{11} \frac{N_{12}^{\ast}}{N_{12}} \frac{d}{dt} \left( i_{1} + N_{12} i_{2} \right) \notag \\ &= \left( L_{11} - \frac{M}{N_{12}} \right) \frac{d i_{1}}{dt} + \frac{M}{N_{12}} \frac{d}{dt} \left( i_{1} + N_{12} i_{2} \right) \label{eq:eqtrans_selfmutual_v1} \\ v_{2} &= \left( 1 - k \frac{N_{12}}{N_{12}^{\ast}} \right) L_{22} \frac{d i_{2}}{dt} + k L_{11} N_{12}^{\ast} \frac{d}{dt} \left( i_{1} + N_{12} i_{2} \right) \notag \\ &= \left( L_{22} - N_{12} M \right) \frac{d i_{2}}{dt} + N_{12} \frac{M}{N_{12}} \frac{d}{dt} \left( i_{1} + N_{12} i_{2} \right) \label{eq:eqtrans_selfmutual_v2} \end{align}

この等価回路は後述する漏れ・励磁インダクタンスを用いた変圧器の等価回路と同じ式であるため、$N_{12}^{\dagger} = N_{12}$とした等価回路の各パラメータは物理的意味を持つ。

等価回路の比較

1次側・２次側漏れインダクタンスを$L_{l1}$、$L_{l2}$、１次側・２次側から見た励磁インダクタンスをそれぞれ$L_{m1}$、$L_{m2}$とする。前回の記事より変圧器のT型等価回路は次式で表すことが可能である。

\begin{align} v_{1} &= L_{l1} \frac{d i_{1}}{dt} + L_{m1} \frac{d}{dt} \left( i_{1} + N_{12} i_{2} \right) \label{eq:eqtrans_leakmag_v1} \\ v_{2} &= L_{l2} \frac{d i_{2}}{dt} + N_{12} L_{m1} \frac{d}{dt}\left( i_{1} + N_{12} i_{2} \right) \label{eq:eqtrans_leakmag_v2} \end{align}

これらの式は自己・相互インダクタンスを用いたT型等価回路の電圧・電流関係式と同じである。また次式を用いて、1次側・２次側漏れインダクタンスと励磁インダクタンスから自己・相互インダクタンスを算出できる。

\begin{align} L_{11} &= L_{l1} + L_{m1} \label{eq:leakmat2selfmutual1} \\ L_{22} &= L_{l2} + L_{m2} \label{eq:leakmat2selfmutual2} \\ M &= N_{12} L_{m1} = \frac{L_{m2}}{N_{12}} \label{eq:leakmat2selfmutual3} \end{align}

式\eqref{eq:eqtrans_selfmutual_v1}-\eqref{eq:eqtrans_leakmag_v2}を比較して次式を得る。これらの式は\eqref{eq:leakmat2selfmutual1}-\eqref{eq:leakmat2selfmutual3}を満たす。

\begin{align} L_{l1} &= L_{11} - \frac{M}{N_{12}} \\ L_{l2} &= L_{22} - N_{12} M \\ L_{m1} &= \frac{M}{N_{12}} \end{align}

よって変圧器の実際の巻き数比$N_{12}$を用いることで、これらの式から自己・相互インダクタンスと漏れ・励磁インダクタンスの相互変換が可能であることがわかる。

漏れ・励磁インダクタンスを用いたT型等価回路は物理的意味が明瞭であり、各インダクタンスと電流・電圧の値を用いて、変圧器内部の磁束を推定することができる。一方で自己・相互インダクタンスを用いたT型等価回路は、等価回路中の理想変圧器の変圧比を任意に与えて1次・２次漏れインダクタンスに相当するインダクタンスを自由に調節した場合でも、簡単に電気回路的に等価な回路を構成可能であるが、この等価回路に物理的意味は無い。

まとめ

この記事では結合インダクタを表現するために頻繁に使用される自己・相互インダクタンス（結合係数）を用いて、変圧器の等価回路を算出した。算出したT型等価回路は等価回路中の理想変圧器の変圧比を任意に与えることで、自由に１次・２次直列インダクタンスの値を調整可能な電気的に等価な回路を得ることが可能である。算出した等価回路と漏れ・励磁インダクタンスを用いた等価回路を比較して、変圧器の実際の巻き数比を用いることで、自己・相互インダクタンスと漏れ・励磁インダクタンスを相互に変換する式を求めた。

参考

1. 石井 聡, 「TNJ-028：トランスのM結合とはナニモノでどのように測るか 前編：理論とシミュレーション」, analog.com, https://www.analog.com/jp/education/landing-pages/003/jp-web-lab/tnj-028.html (Accessed Sep. 28, 2022)
2. 平賀 公久, 「トランスの巻き数と入力／出力電圧の関係」, cc.cqpub.co.jp, https://cc.cqpub.co.jp/system/contents/1652/ (Accessed Sep. 28, 2022)
3. ayumi, 「1.2 トランスの等価回路」, ayumi.cava.jp, http://ayumi.cava.jp/audio/pow/node3.html (Accessed Sep. 28, 2022)
4. 白藤 立, 「第8章 相互インダクタンスと変成器 (変圧器)」, t-shirafuji.jp, http://t-shirafuji.jp/lecture_notes/electric_circuits_i_open/Ch08.pdf (Accessed Sep. 28, 2022)