OpenModelicaを用いたPMSM駆動シミュレーション

前書き

この記事では誰でも無料で使用可能なオープンソースのOpenModelica OMEditを用いた、永久磁石同期モータ（Permanent Magnet Synchronous Motor; PMSM）の電流制御シミュレーションを紹介する。OMEditを用いることで、GUI上で複数の機能ブロックを組み合わせるだけで複雑なシミュレーションを行うことが可能である。PMSMの電流制御では、ベクトル制御による電流フィードバックを実現する。最初にOMEdit上での設定を示した後に、PMSMのベクトル制御による電流フィードバックの理論の概要を説明する。詳細は参考に示したサイトを見てほしい。OMEditでモデルを構成する上で注意が必要なブロックを紹介した後に、シミュレーション結果を示し、モデルの妥当性を確認する。

OpenModelica

OpenModelicaの詳細は他のサイトに任せ、この記事では簡単な説明のみを行う。

概要

OpenModelicaはModelica言語を用いた、オープンソース（OSMC Public License, EPL, GPL）の複雑な動的システムのシミュレーション・モデル作成・最適化・解析の環境であり、誰でも無料で様々な解析をすることができる。OpenModelicaは数学モデルシステム、力学、熱力学、電磁気、電気回路などの幅広い分野のシミュレーションを複合的に行うことが可能である。OpenModelicaの公式ページと、インストール方法について説明しているページを下記に記載するので、参考にしてほしい。

• OpenModelicaの公式ページ
• XSimによるOpenModelicaのインストール方法紹介

OMEdit

OpenModelicaのアプリケーションの1つであるOMEditは、matlab simlinkやscilab xcosのように、GUIを用いて視覚的に機能ブロックを組み合わせることで、シミュレーションモデルを構築できる。この記事ではOMEditを用いて、標準Modelicaライブラリ（Modelica Standard Library; MSL）のみを使うことでPMSMのシミュレーションモデルを構築して、その詳細を説明する。

OMEditで構築したシミュレーションモデルの図と各パラメータの設定値の詳細は下記のPDFに示している。

• シミュレーションモデルとパラメータの設定値（PDF）

PMSM駆動システムモデル

この記事では、空間ベクトル理論を用いて、永久磁石同期モータ（Permanent Magnet Synchronous Motor; PMSM）をインバータによって駆動するシステムを検討する。モータの負荷は定速度負荷とする。インバータは PWM Controller から受け取ったゲート信号$s_{u}$、$s_{v}$、$s_{w}$にしたがって、必要な電圧を出力するように動作する。インバータの入力は直流電圧$V_{DC}$であり、出力は三相電圧$v_{u}$、$v_{v}$、$v_{w}$である。PMSMの前段には電流センサが設置させており、三相電流$i_{u}$、$i_{v}$、$i_{w}$を検出する。PMSMの出力トルクは$T_{m}$、機械角速度は$\omega_{m}$とする。PMSMの機械角$\theta_{m}$は位置センサにより検出される。

制御システムは電流・速度・トルク指令値（Reference）などを入力として、検出した$i_{u}$、$i_{v}$、$i_{w}$と$\theta_{m}$を用いて、PMSMを指令値に追従するように制御する。モータコントローラはPMSMを指令値に追従させるために必要なインバータ出力電圧指令値$v_{u}^{\ast}$、$v_{v}^{\ast}$、$v_{w}^{\ast}$を出力し、PWMコントローラはこれらの指令値を実現するインバータのゲート信号$s_{u}$、$s_{v}$、$s_{w}$を三角波比較法などを用いて生成する。

空間ベクトル理論

PMSMの制御ではゼロ相を制御しないため、クラーク変換を用いて三相電圧・電流をゼロ相とそれ以外の$\alpha$、$\beta$相に分離する。クラーク変換の変換行列$^{0\alpha\beta}\boldsymbol{C}_{uvw}$は次式で定義される。

\begin{equation} ^{0\alpha\beta}\boldsymbol{C}_{uvw} = \sqrt{\frac{2}{3}} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \cos{\left( 0 \right)} & \cos{\left( \frac{2}{3} \pi \right)} & \cos{\left( -\frac{2}{3} \pi \right)} \\ \sin{\left( 0 \right)} & \sin{\left( \frac{2}{3} \pi \right)} & \sin{\left( -\frac{2}{3} \pi \right)} \end{bmatrix} = \sqrt{\frac{2}{3}} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \label{eq:Clark_conv_def} \end{equation}

クラーク逆変換$^{uvw}\boldsymbol{C}_{0\alpha\beta}$は$^{0\alpha\beta}\boldsymbol{C}_{uvw}$を転置することで得られる。

\begin{equation} ^{uvw}\boldsymbol{C}_{0\alpha\beta} = ^{0\alpha\beta}\boldsymbol{C}_{uvw}^{-1} = ^{0\alpha\beta}\boldsymbol{C}_{uvw}^{T} \end{equation}

クラーク変換により得られるゼロ相、$\alpha$相、$\beta$相の電圧・電流をそれぞれ$v_{0}$・$i_{0}$、$v_{\alpha}$・$i_{\alpha}$、$v_{\beta}$・$i_{\beta}$とする。

\begin{equation} \begin{bmatrix} v_{0} \\ v_{\alpha} \\ v_{\beta} \end{bmatrix} = ^{0\alpha\beta}\boldsymbol{C}_{uvw} \begin{bmatrix} v_{u} \\ v_{v} \\ v_{w} \end{bmatrix}, \quad \begin{bmatrix} i_{0} \\ i_{\alpha} \\ i_{\beta} \end{bmatrix} = ^{0\alpha\beta}\boldsymbol{C}_{uvw} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix} \end{equation}

次に、得られた$v_{\alpha}$、$v_{\beta}$、$i_{\alpha}$、$i_{\beta}$を回転子座標系に回転座標変換（dq変換）する。PMSMの極対数を$p_{m}$、電気角を$\theta_{e}$とすると、dq変換行列は次式で与えられる。

\begin{align} \theta_{e} &= p_{m} \theta_{m} \\ ^{dq}\boldsymbol{C}_{\alpha\beta} &= \begin{bmatrix} \cos{\theta_{e}} & \sin{\theta_{e}} \\ -\sin{\theta_{e}} & \cos{\theta_{e}} \end{bmatrix} \label{eq:dq_conv_def} \\ ^{\alpha\beta}\boldsymbol{C}_{dq} &= ^{dq}\boldsymbol{C}_{\alpha\beta}^{-1} = ^{dq}\boldsymbol{C}_{\alpha\beta}^{T} \label{eq:dq_inv_conv_def} \end{align}

逆dq変換行列$^{\alpha\beta}\boldsymbol{C}_{dq}$は\eqref{eq:dq_conv_def}に$\theta_{e} = -\theta_{e}$を代入したものであり、dq変換の逆回転の変換である。よってdq座標系での$\alpha\beta$電圧・電流$v_{d}$、$v_{q}$、$i_{d}$、$i_{q}$は次式で表される。

\begin{equation} \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = ^{dq}\boldsymbol{C}_{\alpha\beta} \begin{bmatrix} v_{\alpha} \\ v_{\beta} \end{bmatrix}, \quad \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} = ^{dq}\boldsymbol{C}_{\alpha\beta} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} \end{equation}

PMSMの数理モデル

uvw座標系において1相当たりの配線抵抗を$R_{uvw}$、永久磁石による磁束の振幅を$\Phi_{uvw}$、電気角速度を$\omega_{e}$とすると、PMSMの数理モデルは次式で表される。

\begin{align} \begin{bmatrix} v_{u} \\ v_{v} \\ v_{w} \end{bmatrix} &= \begin{bmatrix} R_{uvw} & 0 & 0 \\ 0 & R_{uvw} & 0 \\ 0 & 0 & R_{uvw} \end{bmatrix} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix} + \boldsymbol{L} \frac{d}{dt} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix} + \omega_{e} \begin{bmatrix} \Phi_{uvw} \sin{\left( \omega_{e} t \right)} \\ \Phi_{uvw} \sin{\left( \omega_{e} t - \frac{2}{3}\pi \right)} \\ \Phi_{uvw} \sin{\left( \omega_{e} t + \frac{2}{3}\pi \right)} \end{bmatrix} \\ \omega_{e} &= \frac{d \theta_{e}}{dt} \end{align}

ここで$\boldsymbol{L}$はPMSMのインダクタンス行列であり、PMSMの数理モデルの電流微分の係数行列である。上式をdq座標系で表した等価な方程式は次式で表される。

\begin{align} \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} &= \begin{bmatrix} R_{uvw} + L_{d} \frac{d}{dt} & -\omega_{e} L_{q} \\ \omega_{e} L_{d} & R_{uvw} + L_{q} \frac{d}{dt} \end{bmatrix} \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} +  \begin{bmatrix} 0 \\ \omega_{e} \Phi_{dq} \end{bmatrix} \label{eq:PMSM_vi_dq} \\ \Phi_{dq} &= \sqrt{\frac{3}{2}} \Phi_{uvw} \label{eq:Phi_uvw2dq} \end{align}

ここで$L_{d}$、$L_{q}$はd軸・q軸インダクタンスである。dq座標系での配線抵抗はuvw座標系と同じ値$R_{uvw}$となるのに対して、dq座標系での永久磁石の磁束$\Phi_{dq}$はuvw座標系磁束$\Phi_{uvw}$の$\sqrt{3/2}$となることに注意が必要である。

PMSMの制御システム

ここでは古典的な比例積分（PI）制御を適用した電流フィードバック制御をシミュレーションする。PMSMの電流フィードバック制御では、\eqref{eq:PMSM_vi_dq}の干渉項と永久磁石による誘起電圧項をフィードフォワードすることによって補償する。上図は制御ブロック図であり、$i_{d}^{\ast}$、$i_{q}^{\ast}$、$v_{d}^{\ast}$、$v_{q}^{\ast}$は$i_{d}$、$i_{q}$、$v_{d}$、$v_{q}$の司令値である。上図の$i_{d}$、$i_{q}$、$\omega_{e}$はセンサなどにより検出する。司令値$v_{d}^{\ast}$、$v_{q}^{\ast}$は逆dq変換と逆クラーク変換により、$v_{u}^{\ast}$、$v_{v}^{\ast}$、$v_{w}^{\ast}$に変換して PWM Controller に転送する。

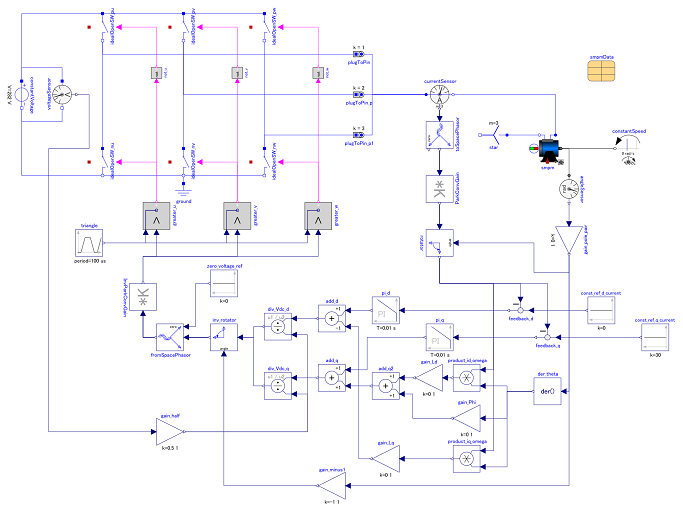
OMEditのPMSM駆動モデルの構築

前述したPMSMドライブ回路とPMSMの制御システムのモデルをOMEditで作成すればよい。ここでは、構築したPMSMのOMEditシミュレーションモデルで注意が必要な要素のみの簡潔な説明を示す（詳細は Modelica Documentation）。 ToSpacePhasor ブロックを用いてクラーク変換を行う場合、\eqref{eq:Clark_conv_def}より、 ToSpacePhasor ブロックの出力値に$\sqrt{3/2}$を乗ずる必要がある。同様に FromSpacePhasor ブロックを使って逆クラーク変換を行うには、ゼロシーケンス値をゼロ相の$1/2$として、ブロックの出力値に$\sqrt{2/3}$を乗ずる。

.Modelica.Electrical.Analog.Ideal.IdealOpeningSwitch
	理想的な開閉スイッチであり、そのスイッチング動作は，入力 boolean 信号により制御される。 boolean 信号が True のときスイッチは OFF となる。
.Modelica.Electrical.Polyphase.Basic.PlugToPin_p
	plug_p （多相回路）の k ピンを pin_p （単相回路）に接続し、plug_p の他のピンは未接続（開放）にする。
.Modelica.Electrical.Machines.SpacePhasors.Blocks.ToSpacePhasor
	多相電圧または電流をスペースフェーザおよびゼロシーケンス値に変換する。三相の場合には、三相入力を$[x_{u}, x_{v}, x_{w}]$、スペースフェーザを$[x_{\alpha}, x_{\beta}]$、ゼロシーケンス値を$x_{0}$とすると、下式の変換を行う。 \begin{align*} \begin{bmatrix} x_{\alpha} \\ x_{\beta} \end{bmatrix} &= \frac{2}{3} \begin{bmatrix} \cos{\left( 0 \right)} & \cos{\left( \frac{2}{3} \pi \right)} & \cos{\left( -\frac{2}{3} \pi \right)} \\ \sin{\left( 0 \right)} & \sin{\left( \frac{2}{3} \pi \right)} & \sin{\left( -\frac{2}{3} \pi \right)} \end{bmatrix} \begin{bmatrix} x_{u} \\ x_{v} \\ x_{w} \end{bmatrix}\\ x_{0} &= \frac{x_{u} + x_{v} + x_{w}}{3} \end{align*}
.Modelica.Electrical.Machines.SpacePhasors.Blocks.FromSpacePhasor
	スペースフェーザおよびゼロシーケンス値から多相電圧または電流へ変換する。三相の場合には、三相出力を$[x_{u}, x_{v}, x_{w}]$、スペースフェーザを$[x_{\alpha}, x_{\beta}]$、ゼロシーケンス値を$x_{0}$とすると、下式の変換を行う。 \begin{equation*} \begin{bmatrix} x_{u} \\ x_{v} \\ x_{w} \end{bmatrix} =\begin{bmatrix} x_{0} \\ x_{0} \\ x_{0} \end{bmatrix} + \begin{bmatrix} \cos{\left( 0 \right)} & -\sin{\left( 0 \right)} \\ \cos{\left( -\frac{2}{3} \pi \right)} & -\sin{\left( -\frac{2}{3} \pi \right)} \\ \cos{\left( \frac{2}{3} \pi \right)} & -\sin{\left( \frac{2}{3} \pi \right)} \end{bmatrix}\begin{bmatrix} x_{\alpha} \\ x_{\beta} \end{bmatrix} \end{equation*}
.Modelica.Electrical.Machines.SpacePhasors.Blocks.Rotator
	スペースフェーザ（電圧または電流）を数学的に負方向（反時計回り）に、入力された角度だけ回転させる。

シミュレーション

OMEditのシミュレーションの刻み幅は$2\mathrm{\mu s}$とした。シミュレーション結果を下記に示す。上から順にdq軸電流$i_{d}$、$i_{q}$とその司令値$i_{d}^{\ast}$、$i_{q}^{\ast}$、uvw相電流$i_{u}$、$i_{v}$、$i_{w}$、uvw相電圧$v_{u}$、$v_{v}$、$v_{w}$、三角波比較での三角波$tri$と変調波$d_{u}$、$d_{v}$、$d_{w}$の波形である。dq軸電流は司令値に追従しており、PMSMの電流制御を実現していることがわかる。uvw相電圧は階段状の波形であり、インバータのPWM制御によりPMSMを制御している。$i_{d}$、$i_{q}$のリプルはスイッチングに起因する。

まとめ

この記事では誰でも無料で使用可能なオープンソースのOpenModelica OMEditを用いた、永久磁石同期モータ（Permanent Magnet Synchronous Motor; PMSM）の電流制御シミュレーションを紹介した。OMEditを用いることで、GUI上で複数の機能ブロックを組み合わせるだけで、数学モデルシステム、力学、熱力学、電磁気、電気回路などの幅広い分野の複雑な動的システムのシミュレーション・モデル作成・最適化・解析を複合的に行うことが可能である。PMSMの電流制御では、ベクトル制御による電流フィードバックを実現して、理論の概要を説明した。OMEditでモデルを構成する上で注意が必要なブロックを紹介した後に、シミュレーション結果を示し、モデルの妥当性を確認した。

参考

• 2022 OpenModelica, 「OpenModelica」, openmodelica.org, https://openmodelica.org/ (Accessed Dec. 17, 2022)
• Adrian Pop, 「OpenModelica Build Server -Modelica Documentation-」, build.openmodelica.org, https://build.openmodelica.org/Documentation/  (Accessed Jan. 5, 2023)
• 一般社団法人オープンCAE学会, 「OpenModelica ユーザーズガイド和訳 リリース v1.14.1」, www.opencae.or.jp, https://www.opencae.or.jp/wp-content/uploads/2021/04/OpenModelicaUsersGuide.pdf
• Wikipedia, 「OpenModelica」, en.wikipedia.org, https://en.wikipedia.org/wiki/OpenModelica
• XSim, 「OpenModelica のインストールと実行」,www.xsim.info,  https://www.xsim.info/articles/OpenModelica/What-is-OpenModelica.html
• 公益社団法人日本電気技術者協会, 「 音声付き電気技術解説講座  電気応用」, jeea.or.jp, https://jeea.or.jp/course/04.html