ハーフブリッジインバータ出力電圧の周波数解析

前書き

パワーエレクトロニクス技術を用いた基本的な電力変換器の1つとして、ハーフブリッジインバータ（HBInv ; Half Bridge Inverter）がある。HBInvは直流入力、単相交流または直流出力可能な変換器であり、HBInvを並列接続することで、任意の相数の出力とすることが可能である。HBInvで任意の出力電圧を実現するために、一般的には三角波比較法を適用したパルス幅変調（PWM ; Pulse Width Modulation）が用いられる。PWMで出力される電圧には、所望の電圧の他に、スイッチングに起因する周波数成分も含まれる。これらの成分は一般的に不要な成分であり、他の機器に影響を及ぼす場合には、フィルタを用いて減衰させる。このフィルタの設計のためにはPWM波形の周波数解析を行い、不要な成分の特性を検討する必要がある。この記事ではHBInvの出力が正弦波の場合のPWM波形について、フーリエ級数展開を用いることで周波数解析を行う。

ハーフブリッジインバータ

回路構成

ハーフブリッジインバータ

上図にハーフブリッジインバータ（HBInv）の回路構成を示す。HBInvは2つのスイッチ$S_{u},S_{l}$から構成される。HBInvの入力は電圧が$E/2$の直流電圧源であり、出力は電流が$i$の電流源である。HBInvの上側の入力電流を$i_{u}$、下側を$i_{l}$、出力端子電圧を$v$としている。スイッチング関数$s_{k}\left(k = u, l\right)$を次式で定義する。

\[ \begin{equation} s_{k} = \begin{cases} 1 & \, \mathrm{スイッチ}S_{k}\mathrm{がON状態} \\ 0 & \, \mathrm{スイッチ}S_{k}\mathrm{がOFF状態} \end{cases} \,,\, k = u, l \end{equation} \]

回路状態

$s_{u}=1,s_{l}=0$

$s_{u}=0,s_{l}=1$

ハーフブリッジインバータ（HBInv）が取りうる回路状態は下記の2つである。

• $s_{u}=1,s_{l}=0$（上側のスイッチがON、下側のスイッチがOFF）
• $s_{u}=0,s_{l}=1$（上側のスイッチがOFF、下側のスイッチがON）

上図は各回路状態でのスイッチの状態と$i > 0$の場合の電流経路（赤線）を示している。したがって、出力電圧$v$はスイッチング行列$S=\begin{bmatrix} s_{u} & s_{l} \end{bmatrix}$を用いて次式で表される。

\[ \begin{equation} v = s_{u} \frac{E}{2} - s_{l} \frac{E}{2} = \begin{bmatrix} s_{u} & s_{l} \end{bmatrix} \begin{bmatrix} \frac{E}{2} \\ -\frac{E}{2} \end{bmatrix} = S \begin{bmatrix} \frac{E}{2} \\ -\frac{E}{2} \end{bmatrix} = \begin{cases} \frac{E}{2} & s_{u}=1,s_{l}=0 \\ -\frac{E}{2} & s_{u}=0,s_{l}=1 \end{cases}\end{equation} \]

一方で、入力電流$i_{u},i_{l}$は次式で得られる。

\[ \begin{equation}\begin{bmatrix} i_{u} \\ i_{l} \end{bmatrix} = \begin{bmatrix} s_{u} \\ s_{l} \end{bmatrix} i = S^{T} i = \begin{cases} \begin{bmatrix} i \\ 0 \end{bmatrix}  & s_{u}=1,s_{l}=0 \\ \begin{bmatrix} 0 \\ i \end{bmatrix} & s_{u}=0,s_{l}=1 \end{cases}\end{equation} \]

ここで$S^{T}$は$S$の転置行列である。

Pulse Width Modulation

PWM波形

上述した通り、ハーフブリッジインバータ（HBInv）の回路状態は２つの状態のいずれかのみとなる。HBInvを任意の電圧を出力可能な電力変換器として動作させるために、一般的にはパルス幅変調（PWM）が用いられる。PWMはパルス波形のパルス幅を変化させることで、１スイッチング周期あたりの平均電圧を制御する変調法である。スイッチング周期$T_{sw}$の期間内で、時間$t_{d}$だけ$s_{u}=1,s_{l}=0$の状態であり、他の期間は$s_{u}=0,s_{l}=1$の状態とする。このとき、１スイッチング周期のHBInvの出力電圧$v$の平均値$\bar{v}$は次式で得られる。

\[ \begin{equation} \bar{v} = \frac{t_{d}}{T_{sw}}\frac{E}{2} - \frac{T_{sw} - t_{d}}{T_{sw}}\frac{E}{2} = \frac{2 t_{d} - T_{sw}}{T_{sw}} \frac{E}{2} \end{equation} \]

ここで、デューティー比$d$を次式で与える。

\[ \begin{equation} d = \frac{t_{d}}{T_{sw}} \; \left( 0 \le d \le 1 \right) \end{equation} \]

このとき、$\bar{v}$は

\[ \begin{equation} \bar{v} = \left( 2 d - 1 \right) \frac{E}{2} \end{equation} \]

となり、パルス幅を決定する変数であるデューティー比$d$を変化させることで、$v$の１スイッチング周期の平均値を$ -E / 2 \le \bar{v} \le E / 2 $の範囲で調整可能である。

三角波比較法

任意のハーフブリッジインバータ（HBInv）の出力電圧平均値$\bar{v}$とするPWM波形を生成する手法として、三角波比較法が用いられる。ここでは$\bar{v}$を次式に示す正弦波とする場合を取り上げる。

\[ \begin{equation} \bar{v} = \alpha \frac{E}{2} \cos{\omega t} \end{equation} \]

ここで$\omega$は出力する正弦波の角周波数、$\alpha$は変調率（$-1 \le \alpha \le 1$）である。出力電圧$\bar{v}$の周期を$T_{out}$とする。

\[ \begin{equation} T_{out} = \frac{2 \pi}{\omega} \end{equation} \]

一般に$T_{out} \gg T_{sw}$に設定する。

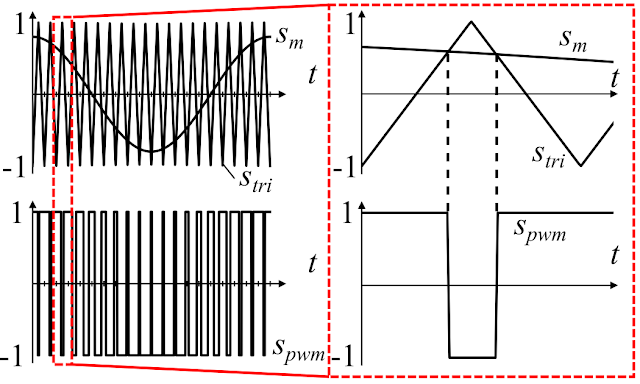
整数$m$に対して、三角波比較法では次式の変調信号$s_{m}$と三角波$s_{tri}$を比較する。

\[ \begin{equation} s_{m} = \alpha \cos{\omega t} \; \left( -1 \le s_{m} \le 1 \right) \end{equation} \]

\[ \begin{equation} s_{tri} = \begin{cases} -1 + \frac{4(t - m T_{sw})}{T_{sw}} & m T_{sw} \le t \le (m + \frac{1}{2}) T_{sw} \\ 3 - \frac{4(t - m T_{sw})}{T_{sw}} & (m + \frac{1}{2}) T_{sw} \le t \le (m + 1) T_{sw} \end{cases} \; \left( -1 \le s_{tri} \le 1 \right) \end{equation} \]

三角波比較法で得られるPWM信号$s_{pwm}$は下記の規則で生成される。

• $s_{m} > s_{tri}$ のとき、$s_{pwm} = 1$とする。
• $s_{m} < s_{tri}$ のとき、$s_{pwm} = -1$とする。

出力電圧$v$と$s_{pwm}$は次式の関係がある。

\[ \begin{equation} v = \frac{E}{2} s_{pwm} \end{equation} \]

よって各スイッチは$s_{u} = (s_{pwm} + 1) / 2$、$s_{l} = (-s_{pwm} + 1) / 2$となるようにON/OFFを制御して、所望の$\bar{v}$を得る。

出力電圧波形の周波数スペクトル

三角波比較法を用いたPWMでは、出力平均電圧$\bar{v}$を所望の値とすることが可能であるが、$v$はパルス状の波形であり、所望の電圧$\bar{v}$に加えて、スイッチング周波数の整数倍の近傍の成分が含まれる。これらの成分は不必要な成分であり、他の機器に影響を及ぼす場合には、フィルタなどを用いて除去する。

三角波比較法を用いたPWMにより生成される$s_{pwm} = v / \left( E / 2 \right)$に含まれる周波数成分は$s_{pwm}$をフーリエ級数展開することにより求められる。出力する所望の正弦波の角周波数を$\omega$、スイッチング角周波数を$\omega_{sw}$とする。

\[ \begin{equation} \omega = 2 \pi f_{out} = \frac{2 \pi}{T_{out}}, \; \omega_{sw} = 2 \pi f_{sw} = \frac{2 \pi}{T_{sw}} \end{equation} \]

変調波$s_{m}$を三角波$s_{tri}$の谷でゼロ次ホールドした場合のPWM信号$s_{pwm}$の複素フーリエ級数展開は次式で表されることが知られている（虚数単位を$i$とする）。

\[ \begin{equation} s_{pwm} = \sum_{mn} a_{mn} \mathrm{e}^{i \Omega_{mn} t} \end{equation} \]

\[ \begin{equation} \Omega_{mn} = m \omega_{sw} + n \omega \end{equation} \]

ここで$m, n$は整数であり、

\[ \begin{equation} a_{mn} = \begin{cases} 0 & \Omega_{mn} = 0 \\ \frac{2}{i \Omega_{mn} T_{sw}} J_{n}\left( \frac{1}{4} \Omega_{mn} \alpha T_{sw} \right) i^{m + n} \left[ \mathrm{e}^{-3 \pi i n \omega / 2 \omega_{sw}} - \left(-1\right)^{m + n} \mathrm{e}^{-\pi i n \omega / 2 \omega_{sw}} \right] & \Omega_{mn} \neq 0 \end{cases} \end{equation} \]

$J_{n} \left( x \right)$は$n$次の第一種ベッセル関数であり、次式で表される。

\[ \begin{equation} J_{n}\left( \frac{1}{4} \Omega_{mn} \alpha T_{sw} \right) = \sum^{\infty}_{k = 0} \frac{\left(-1\right)^k}{k! \Gamma \left( k + n + 1 \right)} \left( \frac{1}{8} \Omega_{mn} M T_{sw} \right)^{ \left(2 k + n  \right)} \end{equation} \]

PWM波形の周波数スペクトル

上式を用いて、$\alpha = 0.9, f_{out} = 50, f_{sw} = 1000$のときの$s_{pwm}の$各スペクトルの振幅を上図に示す。負の周波数のスペクトルは正の周波数に対して周波数が0となる軸で対称なスペクトルとなる。スペクトル図から、PWM信号には、出力する所望の周波数成分の他に、スイッチング周波数の整数倍の近傍にスペクトルが存在する。これらのスペクトルの中には所望の周波数成分と同等の大きさのスペクトルもある。所望の周波数成分以外のスペクトルを除去する場合には、上図のスイッチング周波数の整数倍近傍のスペクトルを十分に減衰可能なフィルタが必要となる。

まとめ

ハーフブリッジインバータ（HBInv）において、三角波比較法を適用したパルス幅変調（PWM）によって出力される電圧には、所望の電圧の他に、スイッチングに起因する周波数成分も含まれる。これらの成分は一般的に不要な成分であり、他の機器に影響を及ぼす場合には、フィルタを用いて減衰させる。この記事ではHBInvの出力が正弦波の場合のPWM波形について、フーリエ級数展開を用いることで周波数解析を行った。PWM波形には所望の周波数成分と同等程度の、スイッチング周波数の整数倍近傍のスペクトルが存在することを確認した。

参考

1. Gregory R. Ainslie-Malik, "Mathematical analysis of PWM processes", Ph.D. thesis, University of Nottingham, 2013, ISNI:0000 0004 2745 9196.
2. 谷口 勝則, 入江 寿一, 石崎 長光：「サイリスタインバータによるPWM電力増幅器」, 電気学会論文誌B, vol. 93, no. 9, 1973.
3. 高橋 勲, 宮入 庄太：「PWMインバータの出力波形とゲート制御信号との関係」, 電気学会論文誌B, vol. 95, no. 2, 1975.

付録

多相インバータ

ハーフブリッジインバータ（HBInv）を並列接続することで、多相出力インバータを実現可能である。多相出力インバータの出力相を$1, 2, \cdots, n, \cdots$として、$n$相のHBInvの上側スイッチを$s_{nu}$、下側スイッチを$s_{nl}$とする。スイッチング行列$S$は次式で定義される。

\[ \begin{equation} S = \begin{bmatrix} s_{1u} & s_{1l} \\ s_{2u} & s_{2l} \\ \vdots & \vdots \\ s_{nu} & s_{nl} \\ \vdots & \vdots \end{bmatrix} \end{equation} \]

出力$n$相の出力端子電圧を$v_{n}$、出力電流を$i_{n}$とする。

このとき、入出力の関係は次式で表すことができる。

\[ \begin{equation} \begin{bmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \\ \vdots \end{bmatrix} = S \begin{bmatrix} \frac{E}{2} \\ -\frac{E}{2} \end{bmatrix} \end{equation} \]

\[ \begin{equation} \begin{bmatrix} i_{h} \\ i_{l} \end{bmatrix} = S^{T} \begin{bmatrix} i_{1} \\ i_{2} \\ \vdots \\ i_{n} \\ \vdots \end{bmatrix} \end{equation} \]